ASVAB Math (MK) Practice Tests & Test Prep by Exam Edge

Pass Your ASVAB Mathematical Knowledge Certification Exam with Exam Edge

Are you nervous about your upcoming ASVAB Mathematical Knowledge certification exam? Look no further, Exam Edge is here to help you achieve your goal! Our world-class online practice certification tests are designed to provide you with the knowledge and confidence you need to pass your ASVAB Math exam on your first try!

Key Facts on Exam Edge's online practice tests for your ASVAB Mathematical Knowledge Exam.

• 20 Online Practice Exams: With Exam Edge, you'll have access to 20 practice tests, each with 50 questions, to help you thoroughly prepare for your ASVAB Math (MK) exam.
• Instant Access: Get started immediately with instant access to your online practice exams. No waiting or software installation is required!
• Detailed Explanations: Each question is accompanied by a detailed explanation, so you'll fully understand the reasoning behind the correct answer and improve your knowledge.
• Take Each Exam 4 Times: You can take our practice exams up to 4 times, giving you plenty of opportunities to review and master the material.
• Web-Based: Our ASVAB practice tests are available 24/7 at your convenience, and because they are web-based, there is no software to install.
• Psychological Advantage: Exam Edge practice tests will allow you to walk into your test day with confidence

Exam Edge practice tests are a valuable tool for helping you prepare for the Armed Services Vocational Aptitude Battery (MK) certification exam. The practice tests provide a realistic simulation of the actual exam, allowing you to become familiar with the format, style, and types of questions you will encounter on the actual test. Certification exams don't just measure what you know -- they are also a test of how well you perform under pressure. The right type of test preparation helps you familiarize yourself not only with the material you're being tested on, but also the format of the test, so you feel less anxiety on test day.

ASVAB Mathematical Knowledge (MK) Exam Prep

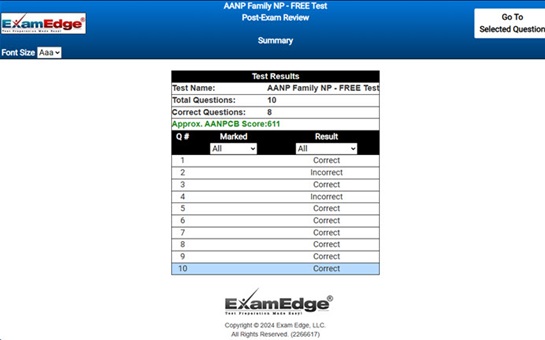
Our comprehensive ASVAB Mathematical Knowledge practice tests are designed to mimic the actual exam. You will gain an understanding of the types of questions and information you will encounter when you take your Armed Services Vocational Aptitude Battery Certification Exam. Our ASVAB Math Practice Tests allow you to review your answers and identify areas of improvement so you will be fully prepared for the upcoming exam and walk out of the test feeling confident in your results.

How to Prepare for the ASVAB Mathematical Knowledge Exam

So, you've decided to pursue your ASVAB Math certification. Not sure what comes next? Follow these steps to register for the exam, craft an effective study plan, and go into test day feeling confident.

Step 1: Check Eligibility and Apply for ASVAB Mathematical Knowledge

Start by researching the testing agency or credentialing organization and the different exams they offer for your field. Before you register for your exam, make sure that the ASVAB Math exam is the right match for your education, experience, and career goals.

Then, check whether you meet the requirements for taking the ASVAB Math exam. You can find eligibility information on the Armed Services Vocational Aptitude Battery website: Armed Services Vocational Aptitude Battery (ASVAB). Once you have determined that you meet the qualifications or have completed the appropriate prerequisites, you can register with the organization and apply to take the ASVAB Math exam.

Step 2: Schedule the ASVAB Math

Once you have registered, you are ready to schedule your exam! The ASVAB Mathematical Knowledge exam is offered at various times throughout the year and at various locations across the United States. You can use the Armed Services Vocational Aptitude Battery website to find a testing center near you and choose a date and time that suits your availability.

When you schedule your ASVAB Math exam, consider how much time you want to study and prepare. Choose a test date that gives you plenty of time to create a study plan, thoroughly review the material, and take several practice tests so that you can go into test day feeling confident and ready. Be sure to schedule your exam well in advance to secure your preferred date and time.

Step 3: Study and Practice for the ASVAB Mathematical Knowledge

After you schedule your test day, dive into your ASVAB Math study plan! Before you crack open a book or start reviewing exam flashcards, take a timed practice test to get a raw baseline of your readiness. As you continue your exam prep, take regular practice tests to track your progress.

Exam Edge practice tests for the ASVAB Math exam offer test-takers key benefits, like helping you identify areas where you need further study and practice. These insights into your test performance will empower you to focus your test prep efforts and prioritize the content areas or skills. This can help you use your study time more effectively and make the most of your efforts before you take the actual exam

Practice tests can also help you to develop your test-taking skills. When you take frequent practice exams, you become more familiar with the format of the ASVAB Mathematical Knowledge exam and learn how to pace yourself throughout it. You will also learn how to approach different types of questions and how to eliminate incorrect answers.

Ultimately, Exam Edge practice tests can help you build your confidence and reduce test-taking anxietyas you become a more comfortable and strategic test-taker. Incorporate ASVAB Math practice exams into your study plan to set yourself up for success on test day

Check out our resources to learn more about ASVAB Math test prep and practice tests.

Step 4: Take the ASVAB Mathematical Knowledge

On the day of the exam, arrive at the test center early to allow plenty of time to check in and get settled at your testing station. You will need to bring at least one valid, government-issued ID with you. Check on the Armed Services Vocational Aptitude Battery (ASVAB) website for other requirements, like:

• Additional forms of identification
• Required materials or supplies
• Other recommended or permitted items, such as water or snacks
• Prohibited items

The website will also include important information about procedures for check-in, security, and breaks, if applicable.

Once you are settled in your seat or at your testing station, take a moment to center yourself and visualize how to ace the ASVAB Mathematical Knowledge exam. Your diligent studying and use of practice tests have prepared you to tackle the exam with confidence. Trust yourself and your exam prep, pace yourself as you have practiced, and have fun showing off what you know!

ASVAB Mathematical Knowledge Exam Prep

Practice tests are a valuable tool for helping you prepare for the ASVAB Math exam.

At Exam Edge, we focus on making our clients' career dreams come true by offering world-class practice tests designed to cover the same topics and content areas tested on the actual ASVAB Math.

Our ASVAB practice tests provide a realistic simulation of the actual exam, allowing you to become familiar with the format, style, and types of questions you will encounter on the actual test.

Happy practicing!

Location Information and Website

For more information on scheduling the Armed Services Vocational Aptitude Battery exam, visit our Armed Services Vocational Aptitude Battery (ASVAB) information page.

---

---